La lotería mas rentable: probabilidades, esperanza matemática y filosofía

La lotería es un impuesto voluntario sobre el desconocimiento de estadística. Esta cita sin autor aparente es usada con frecuencia para descalificar a quienes participan en juegos de azar. La lógica dice que si la esperanza matemática es negativa, la decisión correcta es no jugar. Y por supuesto la esperanza matemática siempre es negativa, porque de lo contrario el emisor de la lotería estaría en quiebra.

Sin embargo, no parece que el juego en loterías decaiga, más bien al contrario. Quizá el motivo no haya que buscarlo en las matemáticas sino en la filosofía. Comprando una participación de lotería no solo se adquiere una pequeña probabilidad de recuperar lo gastado y una remotísima opción de alcanzar la riqueza. No, lo importante no es eso sino la esperanza, ya que la posesión de un billete de lotería proporciona la esperanza, aunque sea temporal, de una solución mágica a todos los problemas.

Una participación de lotería no es un intento desesperado de conseguir dinero fácil, sino una forma sencilla de lograr paz mental. El problema es que esa paz solo dura los días faltantes hasta la celebración del sorteo. Así, la rentabilidad no se mediría en esperanza matemática, que por cierto es la cantidad media recuperada por cada unidad monetaria gastada, sino en el precio de cada día de paz mental logrado con la compra.

Mi conclusión por tanto es que lo importante no es el tamaño del posible premio, ni siquiera la probabilidad de conseguirlo, sino que el precio de la participación sea bajo y, sobre todo, hacer la compra con la mayor antelación posible.

PROBABILIDADES

Pero yo no venía aquí a filosofar, sino a dejar negro sobre blanco cuál es esa esperanza matemática en algunos de los juegos de azar más populares en España.

Como preámbulo, un poco de estadística. La probabilidad de acertar 6 números entre un total de 49 posibles se expresa como el inverso del número de combinaciones posibles, es decir 1/C(49,6). El número de combinaciones C(49,6) se calcula como 49! / (6!x(49−6)!), donde el símbolo ! indica el factorial de un número (3!=3x2x1=6). Cuando la combinación incluye varias elecciones, por ejemplo 6 números de 49 y un reintegro entre 10 disponibles, el número de combinaciones totales es la multiplicación de ambas combinaciones, en el ejemplo sería C(49,6)xC(10,1), y la probabilidad sería el inverso 1 / C(49,6)xC(10,1).

Si no es obligatorio acertar todos los números sino solo 5 aciertos entre los 6 números marcados de entre 49 posibles, y además que el número faltante coincida con el complementario (número adicional elegido entre los no premiados), el número de combinaciones totales es el mismo pero el número de combinaciones ganadoras no es 1 sino C(6,5)xC(1,1), ya que el número elegido no premiado debe coincidir con ese número complementario. Por tanto, la probabilidad no es 1 / C(49,6) sino C(6,5)xC(1,1) / C(49,6).

Por último, para calcular la probabilidad de acertar 5 de los seis números y fallar también el complementario, el número de combinaciones totales sigue siendo el mismo pero el número de combinaciones ganadoras pasa a ser C(6,5)xC(42,1), donde el 42 indica el número de opciones no premiadas eliminando los 6 números ganadores y el complementario. Por tanto, la probabilidad es C(6,5)xC(42,1) / C(49,6).

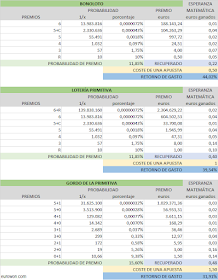
BONOLOTO

Vale, pues vamos al lío. Empecemos con la Bonoloto, que es la más sencilla de calcular por ser simplemente 6 números entre 49 opciones. Las combinaciones posibles son por tanto C(49,6) = 13.983.816.

• Primer premio de 6 aciertos. La probabilidad es 1/C(49,6) = 0,0000071% o una entre casi 14 millones.
• Premio de 5+C (5 aciertos más complementario). La probabilidad es C(6,5)xC(49,1) / C(49,6) = 0,000043% o una entre 2,3 millones.
• Premio de 5 aciertos. La probabilidad es C(6,5)xC(42,1) / C(49,6) = 0,0018% o una entre 55.491.
• ​Premio de 4 aciertos. La probabilidad es C(6,4)xC(42,2) / C(49,6) = 0,096% o una entre 1.032.
• Premio de 3 aciertos. La probabilidad es C(6,3)xC(42,3) / C(49,6) = 1,76% o una entre 57.
• Para el reintegro, por supuesto, la probabilidad es 1 / C(10,1) = 10% o una entre 10.

Sumando todas las probabilidad, tenemos un porcentaje total del 11,85 % de conseguir algún premio.

LOTERÍA PRIMITIVA

Para la Lotería Primitiva se repiten las mismas probabilidades, con la adición de un premio especial que a los seis aciertos suma el reintegro.

• En este premio especial se multiplican las combinaciones posibles hasta 139.838.160, mientras que la probabilidad pasa a ser C(6,6)xC(1,1) / C(49,6)xC(10,1) = 0,00000071% o una entre 139,8 millones.

Sumando todas las probabilidad, tenemos un porcentaje total también del 11,85 % de conseguir algún premio, ya que ese premio especial tiene una probabilidad tan remota que solo altera este porcentaje en el sexto decimal.

GORDO DE LA PRIMITIVA

En el caso del Gordo de la Primitiva cambia la mecánica, pues se escogen 5 números de entre 54 y un número clave entre 10. Así, el número de combinaciones diferentes es C(54,5)xC(10,1) = 31.625.100.

• Primer premio de 5+1 (5 aciertos más el número clave). La probabilidad es 1 / C(54,5)xC(10,1) = 0,0000032% o una entre casi 31,6 millones.
• Segundo premio de 5+0 (5 aciertos sin el número clave). La probabilidad es C(5,5)xC(9,1) / C(54,5)xC(10,1) = 0,000028% o una entre casi 3,5 millones.
• Tercer premio de 4+1. La probabilidad es C(5,4)xC(49,1) / C(54,5)xC(10,1) = 0,00077% o una entre 129.082.
• Cuarto premio de 4+0. La probabilidad es C(5,4)xC(49,1)xC(9,1) / C(54,5)xC(10,1) = 0,007% o una entre 14.342.
• Quinto premio de 3+1. La probabilidad es C(5,3)xC(49,2) / C(54,5)xC(10,1) = 0,037% o una entre 2.689.
• Sexto premio de 3+0. La probabilidad es C(5,3)xC(49,2)xC(9,1) / C(54,5)xC(10,1) = 0,33% o una entre 299.
• Séptimo premio de 2+1. La probabilidad es C(5,2)xC(49,3) / C(54,5)xC(10,1) = 0,58% o una entre 172.
• Séptimo premio de 2+0. La probabilidad es C(5,2)xC(49,3)xC(9,1) / C(54,5)xC(10,1) = 5,24% o una entre 19.
• Octavo premio de 0+1 (Reintegro). La probabilidad es C(1,1) / C(10,1) = 10% restándole la probabilidad de los otros resultados con el número clave (5+1, 4+1, 3+1 y 2+1), dando 9,38 % o una entre 10,66.

Sumando todas las probabilidad, tenemos un porcentaje total del 15,60 % de conseguir algún premio, un porcentaje bastante alto porque hay varios premios relativamente probables.

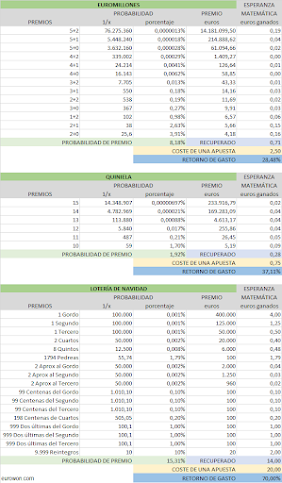
EUROMILLONES

En el caso del Euromillones vuelve a cambiar la mecánica, pues se escogen 5 números de entre 50 y dos números de entre 9. Así, el número de combinaciones diferentes es C(50,5)xC(9,2) = 76.275.360.

• Primer premio de 5+2. La probabilidad es 1 / C(50,5)xC(9,2) = 0,0000013% o una entre 76,2 millones.
• Segundo premio de 5+1 (5 aciertos sin el número clave). La probabilidad es C(5,5)xC(2,1)xC(7,1) / C(50,5)xC(9,2) = 0,000018% o una entre casi 5,4 millones.
• Tercer premio de 5+0. La probabilidad es C(5,5)xC(7,2) / C(50,5)xC(9,2) = 0,000027% o una entre 3,6 millones.
• Cuarto premio de 4+2. La probabilidad es C(5,4)xC(45,1)xC(2,2) / C(50,5)xC(9,2) = 0,00029% o una entre 339.002.
• Quinto premio de 4+1. La probabilidad es C(5,4)xC(45,1)xC(2,1)xC(7,1) / C(50,5)xC(9,2) = 0,0041% o una entre 24.214.
• Sexto premio de 4+0. La probabilidad es C(5,4)xC(45,1)xC(7,2) / C(50,5)xC(9,2) = 0,0062% o una entre 16.143.
• Séptimo premio de 3+2. La probabilidad es C(5,3)xC(45,2)xC(2,2) / C(50,5)xC(9,2) = 0,013% o una entre 7.705.
• Octavo premio de 3+1. La probabilidad es C(5,3)xC(45,2)xC(2,1)xC(7,1) / C(50,5)xC(9,2) = 0,18% o una entre 550.
• Novenopremio de 2+2. La probabilidad es C(5,2)xC(45,3)xC(2,2) / C(50,5)xC(9,2) = 0,19% o una entre 538.
• Décimo  premio de 3+0. La probabilidad es C(5,3)xC(45,2)xC(7,2) / C(50,5)xC(9,2) = 0,27% o una entre 367.
• Undécimo premio de 1+2. La probabilidad es C(5,1)xC(45,4)xC(2,2) / C(50,5)xC(9,2) = 0,98% o una entre 102.
• Duodécimo premio de 2+1. La probabilidad es C(5,2)xC(45,3)xC(2,1)xC(7,1) / C(50,5)xC(9,2) = 2,6% o una entre 38.
• Decimotercer premio de 2+0. La probabilidad es C(5,2)xC(45,3)xC(7,2) / C(50,5)xC(9,2) = 3,91% o una entre 26.

Sumando todas las probabilidad, tenemos un porcentaje total del 4,25 % de conseguir algún premio.

QUINIELA

La probabilidad de acertar en la Quiniela se calcula de forma diferente, ya que la mecánica es muy distinta. En la Quiniela se hacen 15 pronósticos, con un bloque inicial de 14 partidos y un partido adicional que solo se comprueba si se aciertan los 14 primeros, y pudiendo elegir en cada partido entre 3 resultados (1, X o 2). Primero, para calcular la probabilidad de acertar todos los pronósticos según la cantidad de ellos se usan variaciones con repetición, expresadas como x posiciones con y posibilidades, o V (y,x) = y^x.  Después, para calcular el número de combinaciones posibles de x pronósticos dentro de 14 partidos, se usa la misma fórmula de combinaciones de las loterías anteriores. Todo esto, por supuesto, asumiendo que es un juego puramente de azar y ningún resultado es más probable que otro, lo cual claramente no es cierto para las personas aficionadas al fútbol.

• Pleno al 15. La probabilidad es C(15,15)/V(3,15) o una entre 14.348.907.
• 14 aciertos. La probabilidad es C(14,14)/V(3,14) o una entre 4.782.969.
• 13 aciertos. La probabilidad es C(14,13)/V(3,13) o una entre 113.880.
• 12 aciertos. La probabilidad es C(14,12)/V(3,12) o una entre 5.480.
• 11 aciertos. La probabilidad es C(14,11)/V(3,11) o una entre 487.
• 10 aciertos. La probabilidad es C(14,10)/V(3,10) o una entre 59.

Sumando todas las probabilidad, tenemos un porcentaje total del 1,92 % de conseguir algún premio. Insisto en que este cálculo supone completa aleatoriedad en los resultados.

LOTERÍA DE NAVIDAD

Para la Lotería de Navidad, por cierto, el cálculo es todavía más sencillo. Si se emiten 100.000 números  y cada número va al bombo, la probabilidad de cada premio es proporcional a la cantidad de números premiados. Todo esto independientemente del número de series por número.

• Gordo (1 premio). La probabilidad es una entre 100.000.
• Segundo (1 premio). La probabilidad es una entre 100.000.
• Tercero (1 premio). La probabilidad es una entre 100.000.
• Cuartos (2 premios). La probabilidad es una entre 50.000.
• Quintos (8 premios). La probabilidad es una entre 12.500.
• Pedreas (1.794 premios). La probabilidad es una entre 55,74.
• Aproximaciones al Gordo (2 premios). La probabilidad es una entre 50.000.
• Aproximaciones al Segundo (2 premios). La probabilidad es una entre 50.000.
• Aproximaciones al Tercero (2 premios). La probabilidad es una entre 50.000.
• Centenas del Gordo (99 premios). La probabilidad es una entre 1.010,1.
• Centenas del Segundo (99 premios). La probabilidad es una entre 1.010,1.
• Centenas del Tercero (99 premios). La probabilidad es una entre 1.010,1.
• Centenas de los Cuartos (198 premios). La probabilidad es una entre 505,05.
• Dos últimas cifras del Gordo (999 premios). La probabilidad es una entre 100,1.
• Dos últimas cifras del Segundo (999 premios). La probabilidad es una entre 100,1.
• Dos últimas cifras del Tercero (999 premios). La probabilidad es una entre 100,1.
• Reintegros (9.999 premios). La probabilidad es una entre 10.

Sumando todas las probabilidad, tenemos un porcentaje total del 15,31 % de conseguir algún premio. Por este motivo es el sorteo favorito de casi todos. Bueno, por este motivo y por uno más poderoso todavía que es el miedo a ser el único sin premio en un grupo de amigos, vecinos o compañeros de lo que sea.

ESPERANZA MATEMÁTICA

Ahora que ya tenemos calculados los porcentajes de probabilidad de cada premio, para calcular la esperanza matemática de cada tipo de lotería hay que considerar otros dos factores. Primero, el precio de una apuesta. Y segundo, el montante medio de cada premio, para lo cual tomaré la media de los últimos diez sorteos.

El resultado se muestra en las siguiente tablas.

Como se puede ver, si tenemos en cuenta la esperanza matemática de retorno del gasto, lo más "rentable" (entre comillas muy grandes) es jugar a la Lotería de Navidad. Y de entre las loterías por combinaciones, la más "rentable" (más comillas gordas) es la Bonoloto, curiosamente un sorteo poco popular por la percepción de que los premios son pequeños. Mención aparte para la quiniela, que no se queda tan lejos y puede ser una opción interesante para futboleros (pero ojo que Dunning-Kruger no hace prisioneros).

Espero que el ejercicio te haya resultado entretenido. Como nota final, decir que esto no supone recomendación de participación en ningún sorteo. Lo más rentable siempre será hacer aportaciones periódicas a un índice global como el MSCI World o similar. John Bogle no jugaba a la lotería.

→ Al preparar este post me he apoyado en esta web de cálculo estadístico.

COMPARTIR ES BUENO

Tweet

COMPRA MI LIBRO
CUENTOS INFANTILES
CON FINAL MACABRO

PRACTICA GRATIS VOCABULARIO
DE COREANO E INGLÉS
→ MANSIGAN.COM ←

Si te ha gustado este post, puedes ayudarme a mejorar con un pequeño gesto :)
→ CLICK AQUÍ ←